முக்கோணவியல் அடையாளங்கள் என்பது ஒரு வடிவியல் உருவத்தில் காணக்கூடிய மாறி முக்கோணவியல் செயல்பாடுகளைக் குறிக்க கணிதத் துறையில் பயன்படுத்தப்படும் ஒரு கருத்தாகும். முக்கோணவியல் என்பது கணிதத்தின் ஒரு கிளை ஆகும், இது முக்கோணங்களின் பகுப்பாய்வு மற்றும் ஆய்வுகளில் நிபுணத்துவம் பெற்றது, குறிப்பாக பல்வேறு கோணங்களின் வடிவங்கள், அர்த்தங்கள் மற்றும் மதிப்புகள். முக்கோணவியல் அடையாளங்கள், ஒன்றிலிருந்து மற்றொன்றுக்கு மாறுபடும் மற்றும் மிகவும் மாறுபட்ட மதிப்புகளின் விளைவாக இருக்கும்.
கணிதத்தின் பல கூறுகளைப் போலவே, பண்டைய காலங்களிலிருந்து கருத்துக்கள் உள்ளன, இதில் கிரேக்க தத்துவவாதிகள் ஏற்கனவே வடிவியல் உருவங்களின் கோணங்களின் செயல்பாடுகள் மற்றும் மதிப்புகள் பற்றிய கருத்துக்களை நிறுவியுள்ளனர். இந்த கருத்துக்கள் நவீனத்துவத்தில் மட்டுமே மேம்படுத்தப்படும், பதினேழாம் நூற்றாண்டில் பல்வேறு கோணங்களுக்கு இடையில் அனைத்து வகையான கணக்கீடுகளையும் செய்ய இயற்கணித ரீதியாக அவை குறிப்பிடப்பட்டன.
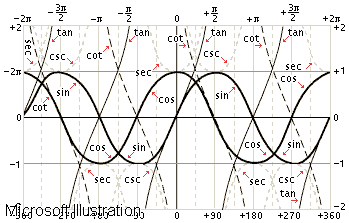
முக்கோணவியல் அடையாளங்கள் ஒரு வடிவியல் உருவத்தில் இருக்கக்கூடிய அனைத்து சாத்தியமான கோண மாறிகள் என பரந்த அளவில் வரையறுக்கப்படலாம். இந்த அடையாளங்கள் எப்போதும் ஆல்பா, பீட்டா, ஒமேகா போன்ற கிரேக்க எழுத்துக்களில் இருந்து குறிப்பிடப்படுகின்றன. ஒவ்வொரு அடையாளத்தின் மாறிகளையும் நிறுவ டிகிரி சென்டிகிரேட் போன்ற கூறுகளும் பயன்படுத்தப்படுகின்றன. சைன் மற்றும் கோசைன், சைன் மற்றும் டேன்ஜென்ட் போன்றவற்றுக்கு இடையே நிறுவப்பட்டவை மிகவும் பிரபலமானவை. முக்கோணவியல் அடையாளங்கள் எளிமைப்படுத்தப்பட்ட வடிவங்கள் ஆகும், அவை முக்கோணவியலின் வெவ்வேறு செயல்பாடுகளைச் செய்யவும் அறியவும் அனுமதிக்கிறது. கணிதத்தின் இந்தக் கேள்விகள் அனைத்தும், குறிப்பாக முக்கோணவியல், ஒவ்வொரு வகை தரவுகளின் குறிப்பிட்ட செயல்பாடுகளிலிருந்து மேற்கொள்ளப்பட வேண்டிய வெவ்வேறு கணக்கீடுகளை ஒழுங்கமைக்க உதவுகிறது. முக்கோணவியல் அடையாளங்கள் மிகவும் மாறக்கூடியவை மற்றும் ஒவ்வொரு முக்கோணவியல் செயல்பாட்டையும் (அதாவது, மதிப்புகள்) வெவ்வேறு மற்றும் குறிப்பிட்ட வழிகளில் ஒவ்வொரு வழக்கின் படியும் பிரதிநிதித்துவப்படுத்த வெவ்வேறு சாத்தியக்கூறுகளை அனுமதிக்கின்றன.
